In my experience taking solid state physics classes, esoteric concepts are constantly presented like they’re completely self-evident. Of course, the dispersion relation of a material lays out valuable information that you understand immediately. Of course. Maybe you had a clearer professor than I did, but if you didn’t, I’ll cover my understanding of these concepts starting from the bottom and bringing in minimal math to paint a conceptual picture. In this science story time, I’m going to take a step back and start with wavevectors and the nature of vibrations on clotheslines, explain what phonons are, and then go into what a dispersion relation is and what they can tell you. This post will focus on phonon dispersion relations because electrons are weirder and more annoying than phonons are. They demand their own post.
The wavevector, usually denoted as k, is the spatial frequency of a wave and points in the direction the wave is going. Imagine a clothesline. The wavevector k tells you how many full wavelengths are on that clothesline. Depending on whether you are a physicist or a crystallographer (my condolences to those who are both), there might be a factor of 2π involved, but it’s a matter of taste for our conceptual picture.
Why not just use wavelength? Well, k is directly proportional to the energy in that wobbly clothesline, so it’s easier to think about. Ah yes, big k means big energy, good. You nod, satisfied.


Two clotheslines. The left clothesline is a low k vibration, since it only has half of a wavelength. The right clothesline is a higher k vibration with 5 full wavelengths. You’d have to work a lot harder to get a clothesline into the blue configuration than the red one.
When most people talk about the frequency of a wave, they aren’t talking about the spatial frequency k but the temporal frequency, usually expressed as ω, which is cycles per second with units of Hertz. The temporal frequency is how fast the amplitude of the wave oscillates up and down. The two waves shown above have the same ω value but different k values, while the two waves shown below have the same k value but different ω values. A dispersion relation, which I’ll go into more detail about later, essentially plots inverse space (k, the spatial frequency) vs inverse time (ω, the temporal frequency).


These two clotheslines have the same k value but different ω values. Clearly, the line on the right is oscillating faster than the one on the left, so it has a higher ω.
Now instead of a clothesline, imagine atoms arranged in a line. Unlike the string, which you can rattle as hard as you want to your heart’s content (or the limitations of your upper body strength), there is a maximum value of k that can’t be exceeded by the line of atoms. The highest k is achieved when each atom in the line is going in opposite directions from its nearest neighbors.


The left line of atoms is the lowest k value (k = 0), achieved when all of the atoms move together. The right line of atoms is the highest k value possible (k = 2π/a). That 2π is optional but the a for the distance between atoms isn’t. Atoms don’t move this much in reality; this is grossly exaggerated for the sake of the story.
So far, this analogy of actually moving atoms up and down works for phonons. Phonons are quantized mechanical vibrations, in the same way that photons are quantized light. The discrete nature of crystal lattices (repeating arrangements of atoms instead of continuous clotheslines) as well as the specific structure of the unit cell selects a limited range of possible frequencies for phonons to vibrate at. While photons can act like point particles and be concentrated into a small area, phonons are physically spread across the entire crystal lattice. Technically, moving a block of metal moves all of the atoms in it simultaneously, the same as the k = 0 phonon mode.
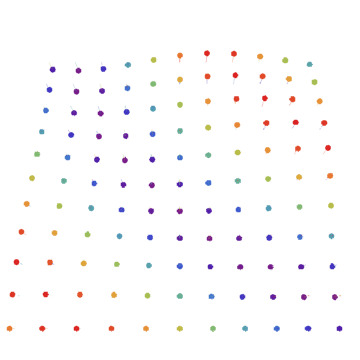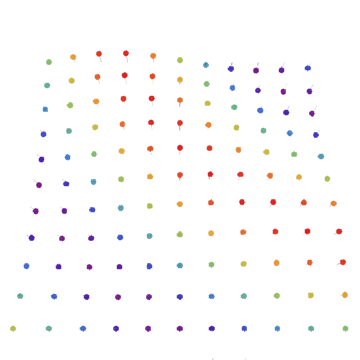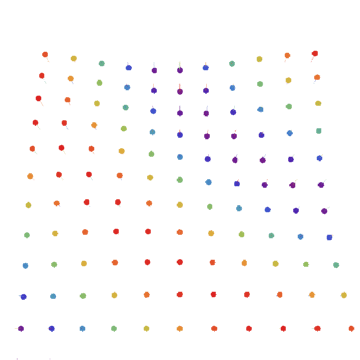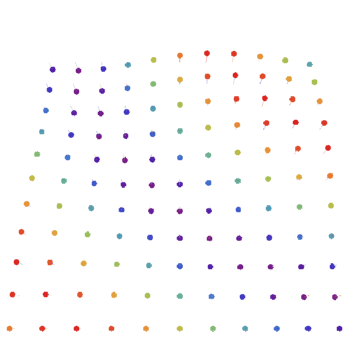
A phonon in a 2D lattice. We’ve upgraded from plucking clotheslines to rippling sheets. The phonon encompasses the entire lattice and cannot be physically localized like a particle, but phonons do still have some particle-like properties.
Phonons still exist in other types of materials besides crystalline solids, such as polymers, some liquids, and many molecular compounds. These phonon modes are no longer as straightforward as clotheslines rippling through our nice theoretical infinite crystal lattice, but are present instead as bending, breathing, stretching, and other yoga-inspired modes based on the various ways the atoms of the system contort themselves. Techniques like Raman and IR spectroscopy can identify unknown compounds by mapping the energies of their phonon modes, which acts like a unique “molecular fingerprint”.
Besides identification, phonons determine a number of useful properties. They are the main carriers of heat and determine how fast the speed of sound will propagate through a material. Side note: In crystals, phonons can also vibrate longitudinally, which clotheslines can’t really do. The clothesline metaphor can only be stretched so far, alas.

The left line of atoms is an example of a transverse oscillation, where the atoms move perpendicular to the line connecting them. Similarly, the right line of atoms is an example of a longitudinal oscillation, where the atoms move parallel to the line connecting them. Strings don’t really “do” longitudinal oscillations, c’est la vie.
Onward to dispersion relations.
Generally the branches in a dispersion relation graph look like spaghetti. An example of a phonon dispersion relation with separate longitudinal and transverse branches (or spaghetti noodles) is shown below.
![]()
This is a phonon dispersion relation for silicon. The letters along the x-axis denote a crystallographic direction that the “phonon clothesline” of atoms lies along. TA/LA = transverse/longitudinal acoustic phonons, aka the mechanical vibrations we’ve talked about so far. TO/LO = transverse/longitudinal optical phonons, aka phonons that can be excited by incoming light waves and are higher frequency than mechanical vibrations. From this paper.
A dispersion relation plots ω as a function of k, or how the energy of a phonon changes with its shape. This essentially tells you how the material mucks with the waves within it. As a non-phonon example, white light travelling through vacuum has a completely linear dispersion relation, meaning that every wavelength contained in the white light is unmucked with and travels at the same speed, our friend c. However, when the light passes through something interesting, like a glass prism, the dispersion relation is no longer linear. Different wavelengths of light couple with the glass differently. The intensity of coupling changes the travelling speed, which separates out the white light into its constituent colors. Voila. A rainbow.

Whoa.
Back to phonons.
The slope of a phonon branch in a dispersion relation is the group velocity, which is how fast the phonon at that value of k can propagate constructively through the material. Phonons at the boundaries of the unit cell have undefined or flat slopes, which signify that they either move the entire solid (k = 0) or are standing waves (when each atom moves opposite of its neighbor, k = 2π/a). In either case, these phonons do not propagate through the lattice and so they cannot transfer heat or sound.
For low values of k in the acoustic phonon branches, the branch is essentially linear and the group velocity represents the speed of sound. Steep phonon branches that are close to the thermal energy of room temperature (~0.026 eV or ~ 38 THz) are best for thermal conductivity applications. Some materials have phonon bandgaps, which is a band of energies between branches with no phonon modes present. Any external incident phonons within these forbidden energies would be completely reflected by the material while any internally generated forbidden phonon modes would be trapped and completely unable to propagate. A thermal insulator.
The energy ranges of a given phonon branch are determined by the same factors that determine how elastic a spring is: how heavy the atoms are and how strong the bonds connecting them are. In our clothesline analogy, the atomic mass is how heavy the string is while the bond strength is the tension of the string.
Taut, straight, light strings and few defects -> Increased thermal conductivity
Conversely,
Loose, squiggly, heavy strings and tons of weird obstacles -> Bad thermal conductivity
Thermoelectrics research is looking to engineer materials that have low heat conductivity but high electrical conductivity or vice versa, which would allow the fabrication of devices to generate electricity from waste heat. Another important area of research is high k dielectrics (k in this case isn’t the wavevector like we’ve been using, but the dielectric constant k which is essentially how polarizable an insulating material is) which aims for a nanoscale, light, and ideally flexible high k dielectric to prevent leakage current in tiny electronic components. As an example, diamond is an electric insulator that has very strong covalent bonds with a light element (carbon has an atomic number of only 6), so it isn’t surprising that it has a thermal conductivity five times better than copper. Sadly, diamond is not very elastic, but you can hopefully now understand the trade-off between elasticity and thermal conductivity.
Finally, density of states (DOS) diagrams arise directly from dispersion relations and illustrate how many phonon modes exist in a given energy range. This allows an enterprising researcher to eyeball if a given material is likely to be a good thermal conductor or not for a temperature range of interest. Having more states (a taller peak in the DOS) around the thermal frequency range of a given temperature means that the material will be more thermally conductive at that temperature. Similarly, bandgaps in the DOS diagram show energy ranges where the material is thermally insulating, which can also be useful.
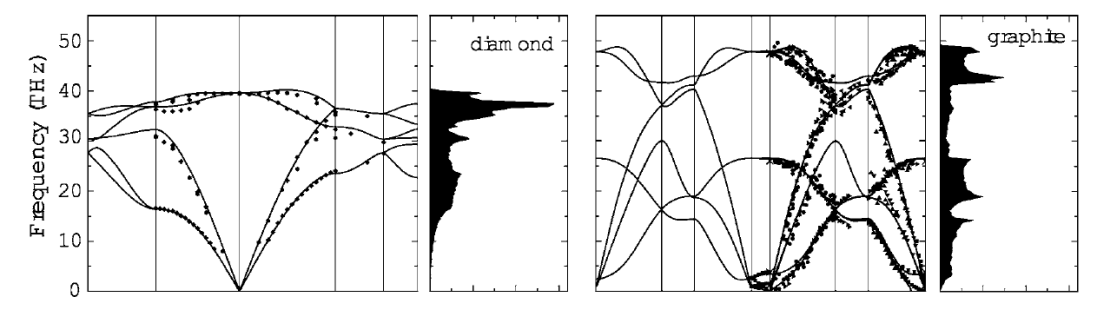
Diamond is one of the best thermally conductive materials currently known. Graphite has strong thermal conductivity along the 2D graphene sheets that compose its structure, but between the sheets the thermal conductivity drops precipitously, so on average graphite is just okay overall. From this paper.
If you’re really into acoustics you may feel a bit short changed by my focus on thermal conductivity. Sorry, I just think heat is cooler.